最先创立微积分的人是谁？微积分（Calculus），数学概念，是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科，内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。下面就跟360常识网一起具体看看最先创立微积分的人等相关内容。

最先创立微积分的人

微积分的创立有它的历史条件，它是在16、17世纪自然科学蓬勃发展，特别是力学、运动学的发展向数学提出了新的要求而引起的。1590年，刻卜勒发现行里绕太阳运动的轨道是椭圆。这些都要求人们用数学方法表示这些轨道外对这些图形的性质作深人的研究。正是为了解决这些迫切的问题,笛卡尔先建立了坐标法，第一次引进了“变数”。在笛卡尔坐标内，一条曲线就被看作是一个运动的点和代数学上的一对变数建立起来的一一对应的关系，使运动和变化的概念进人了数学，从而创立了解析几何学，为微积分的出现建立了第个决定性步骤。然而,解析几何所研究的对象毕竟还只是几何图形或变量间的对应关系，却不能表示和刻划出当时其他科学向数学提出的以下四种类型的问题：①已知物体移动的距离表示为时间的函数的公式,求物体在任意时刻的速度、加速度及其逆问题;②求曲线的切线;③求函数的最大值和最小值;④求曲线长，曲线围成的面积，曲面围成的体积,物体的重心。牛顿(左上图）从研究物体运动的速度人手,企图解决这些问题;莱布尼兹(右上围)从研究曲线的斜率人手,企图解决这些问题。其结果,两人都得到了导数，即都用变化的观点，引进变化的量和极限概念,研究变化舂的运动。用导数可以表示一瞬间的动态,刻划出物体运动的规律，使历史上各种求切线、面积、体积和物体重心的问题得到了统一的处理。导数出现后，微积分逐步发展完善。从此，自然科学才可运用数学不仅表明状态，并且也表明过程,即运动。

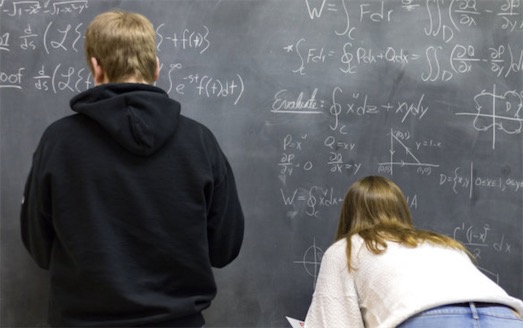
那么，牛顿和莱布尼兹两人中是谁先创微枳分的呢？为这个问题,英国数学界和法国数学界曾经进行过激烈的争论。法、德数学家支持萊布尼兹,而英国数学家支持牛顿。激烈的争论曾使两国数学家在一段时期内断绝了往来。

1687年以前，牛顿并没有正式发表过行关微枳分的论文。但是，牛顿在1665一1687年，曾把自己研究的结果通知朋友；在1669年,牛顿把题为(运用无穷多项方程的分析学>的小册子分送给自己的朋友。1669年，牛顿把这本书送给布朗教授，后来乂送给莱布尼兹的朋友柯串斯。直到1771年，这本书才正式出版。

莱布尼兹于1672年访问巴黎，1673肀访问伦敦,并且和一些知道牛顿工作的数学家通信。到1684年，莱布尼兹正式发表了微积分的著作。于是，英国数学家指责莱布尼兹是剽窃者。

这场争论直到他们逝世之后j结束。通过调查，原来牛顿和莱布尼兹都受布朗教授的许多启发，先后独立地在研究问題时建立了微枳分，只不过一个是工作做得早，个是论文发表得早。因此，牛顿和莱布尼兹都是最早创立微枳分的人。

微积分（Calculus），数学概念，是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科，内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。微积分历史

从微积分成为一门学科来说，是在17世纪，但是积分的思想早在古代就已经产生了。

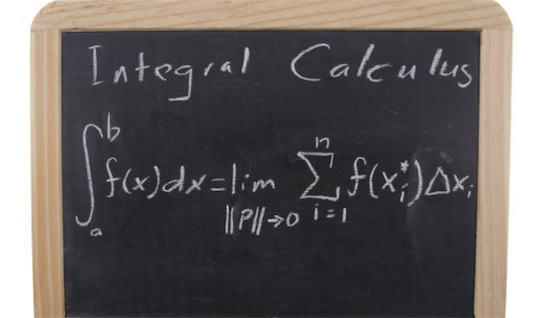
积分学早期史

公元前7世纪，古希腊科学家、哲学家泰勒斯就对球的面积、体积、与长度等问题的研究就含有微积分思想。公元前3世纪，古希腊的数学家、力学家阿基米德（公元前287~前212）的著作《圆的测量》和《论球与圆柱》中就已含有积分学的萌芽，他在研究解决抛物线下的弓形面积、球和球冠面积、螺线下的面积和旋转双曲线所得的体积的问题中就隐含着近代积分的思想。

中国古代数学家也产生过积分学的萌芽思想，例如三国时期的刘徽，他对积分学的思想主要有两点：割圆术及求体积问题的设想。

转载请注明来源：360常识大全网 http://www.360changshi.com/